Contoh Soal Kuartil Data Kelompok
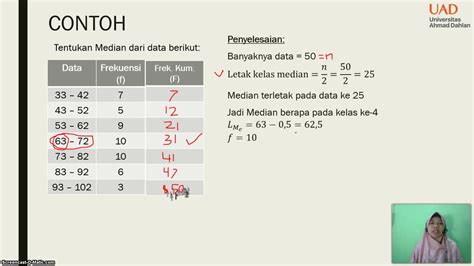
Bingung bagaimana menghitung kuartil pada data kelompok? Artikel ini akan memberikan Anda contoh soal contoh soal kuartil data kelompok lengkap dengan penyelesaiannya, sehingga Anda dapat memahami konsep ini dengan mudah. Mari kita mulai!
Memahami Kuartil Data Kelompok
Kuartil data kelompok merupakan nilai yang membagi data terurut menjadi empat bagian yang sama besar. Ada tiga kuartil, yaitu:
- Kuartil pertama (Q1): Membagi 25% data terkecil dari 75% data terbesar.
- Kuartil kedua (Q2): Sama dengan median, membagi data menjadi dua bagian sama besar.
- Kuartil ketiga (Q3): Membagi 75% data terkecil dari 25% data terbesar.
Menghitung kuartil pada data kelompok sedikit berbeda dengan data tunggal karena kita perlu mempertimbangkan interval kelas.
Contoh Soal Kuartil Data Kelompok
Berikut ini adalah contoh soal contoh soal kuartil data kelompok yang akan kita selesaikan bersama:
Berikut data berat badan (dalam kg) dari 20 siswa:
| Berat Badan (kg) | Frekuensi | Frekuensi Kumulatif |
|---|---|---|
| 40 - 44 | 3 | 3 |
| 45 - 49 | 5 | 8 |
| 50 - 54 | 7 | 15 |
| 55 - 59 | 3 | 18 |
| 60 - 64 | 2 | 20 |
Tentukan Q1, Q2, dan Q3 dari data tersebut!
Penyelesaian:
* Letak Q1 = (1/4) x N = (1/4) x 20 = 5
* Letak Q2 = (2/4) x N = (2/4) x 20 = 10
* Letak Q3 = (3/4) x N = (3/4) x 20 = 15
* Q1 (Letak 5): Q1 terletak pada kelas interval 45 - 49. Kita gunakan rumus:
Q1 = L + [( (N/4) - Fk ) / f ] x c
Dimana:
* L = batas bawah kelas interval Q1 (44.5)
* N/4 = 5 (letak Q1)
* Fk = frekuensi kumulatif sebelum kelas interval Q1 (3)
* f = frekuensi kelas interval Q1 (5)
* c = panjang kelas interval (5)
Q1 = 44.5 + [ (5 - 3) / 5 ] x 5 = 44.5 + 2 = 46.5
* Q2 (Letak 10): Q2 terletak pada kelas interval 50 - 54. Kita gunakan rumus yang sama, dengan N/4 diganti menjadi N/2 = 10:
Q2 = 49.5 + [ (10 - 8) / 7 ] x 5 = 49.5 + 1.43 = 50.93
* Q3 (Letak 15): Q3 terletak pada kelas interval 50 - 54. Kita gunakan rumus yang sama, dengan N/4 diganti menjadi 3N/4 = 15:
Q3 = 49.5 + [ (15 - 8) / 7 ] x 5 = 49.5 + 5 = 54.5
Jadi, Q1 = 46.5 kg, Q2 = 50.93 kg, dan Q3 = 54.5 kg.
Kesimpulan
Menghitung contoh soal kuartil data kelompok memerlukan pemahaman rumus dan identifikasi kelas interval yang tepat. Dengan latihan yang cukup, Anda akan mahir dalam menghitung kuartil data kelompok. Semoga contoh soal ini membantu Anda!
Tanya Jawab
Q: Apa perbedaan menghitung kuartil pada data tunggal dan data kelompok?
A: Pada data tunggal, kuartil dapat langsung ditentukan dengan mengurutkan data. Sedangkan pada data kelompok, kita perlu mempertimbangkan interval kelas dan menggunakan rumus interpolasi untuk menghitung nilai kuartil.
Q: Apa pentingnya mengetahui kuartil dalam statistika?
A: Kuartil memberikan gambaran tentang penyebaran data dan membantu dalam menganalisis distribusi data. Kuartil juga digunakan untuk mengidentifikasi outlier dan menghitung jangkauan interkuartil.
Q: Apa yang dimaksud dengan jangkauan interkuartil (IQR)?
A: Jangkauan interkuartil (IQR) adalah selisih antara Q3 dan Q1 (IQR = Q3 - Q1). IQR memberikan gambaran tentang penyebaran data di tengah-tengah distribusi.
Semoga penjelasan ini bermanfaat! Jangan ragu untuk bertanya jika masih ada yang kurang jelas.





