Contoh Soal Panjang Busur: Panduan Lengkap

2025-02-15 by admin
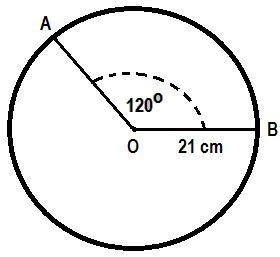
Contoh Soal Panjang Busur: Panduan Lengkap

Contoh Soal Panjang Busur dan Pembahasannya

Artikel ini akan membahas berbagai contoh soal panjang busur lingkaran, mulai dari yang sederhana hingga yang lebih kompleks. Anda akan belajar cara menghitung panjang busur dengan memahami konsep sudut pusat dan keliling lingkaran. Siap mengasah kemampuan matematika Anda? Mari kita mulai!

Rumus Panjang Busur

Sebelum masuk ke contoh soal panjang busur, mari kita ingat kembali rumus dasarnya. Panjang busur (P) dapat dihitung dengan rumus:

`

P = (θ/360°) x 2πr

`

di mana:

    1. P = panjang busur

    2. θ = sudut pusat (dalam derajat)

    3. r = jari-jari lingkaran

      4. Rumus ini berlaku untuk lingkaran dengan sudut pusat yang dinyatakan dalam derajat. Jika sudut pusat dinyatakan dalam radian, rumusnya menjadi:

      `

      P = θr

      `

      di mana θ adalah sudut pusat dalam radian.

      Contoh Soal Panjang Busur 1: Sederhana

      Soal: Sebuah lingkaran memiliki jari-jari 7 cm. Hitunglah panjang busur lingkaran tersebut jika sudut pusatnya 60°.

      Penyelesaian:

      Kita gunakan rumus: P = (θ/360°) x 2πr

    4. θ = 60°

    5. r = 7 cm

    6. π ≈ 22/7

      7. P = (60°/360°) x 2 x (22/7) x 7 cm

      P = (1/6) x 44 cm

      P = 22/3 cm ≈ 7,33 cm

      Jadi, panjang busurnya sekitar 7,33 cm.

      Contoh Soal Panjang Busur 2: Mencari Sudut Pusat

      Soal: Sebuah lingkaran memiliki jari-jari 10 cm dan panjang busur 5π cm. Tentukan besar sudut pusatnya!

      Penyelesaian:

      Kita gunakan rumus: P = (θ/360°) x 2πr dan kita cari θ.

    7. P = 5π cm

    8. r = 10 cm

    9. π ≈ 3.14

      10. 5π = (θ/360°) x 2π x 10

      5π = (θ/360°) x 20π

      5 = (θ/360°) x 20

      θ = (5 x 360°) / 20

      θ = 90°

      Jadi, besar sudut pusatnya adalah 90°.

      Contoh Soal Panjang Busur 3: Lingkaran dengan Jari-jari yang Tidak Diketahui

      Soal: Panjang busur suatu lingkaran adalah 12 cm dan sudut pusatnya 60°. Berapakah jari-jari lingkaran tersebut?

      Penyelesaian:

      Kita gunakan rumus: P = (θ/360°) x 2πr dan kita cari r.

    10. P = 12 cm

    11. θ = 60°

    12. π ≈ 3.14

12 = (60°/360°) x 2 x 3.14 x r

12 = (1/6) x 6.28 x r

r = (12 x 6) / 6.28

r ≈ 11.46 cm

Jadi, jari-jari lingkaran tersebut sekitar 11.46 cm.

Tanya Jawab Seputar Panjang Busur

Q: Apa perbedaan antara panjang busur dan keliling lingkaran?

A: Keliling lingkaran adalah panjang keseluruhan lingkaran, sedangkan panjang busur hanya merupakan sebagian dari keliling tersebut, yang dibentuk oleh sudut pusat tertentu.

Q: Bagaimana jika sudut pusat diberikan dalam radian?

A: Gunakan rumus P = θr, di mana θ adalah sudut pusat dalam radian dan r adalah jari-jari lingkaran.

Q: Apakah ada contoh soal panjang busur yang lebih kompleks?

A: Tentu! Contoh soal bisa melibatkan lebih banyak variabel atau berkaitan dengan bangun ruang seperti kerucut atau bola. Anda dapat mencari contoh soal lebih lanjut di buku teks matematika atau sumber belajar online lainnya.

Semoga contoh soal panjang busur di atas membantu Anda memahami konsep dan cara menghitungnya. Jangan ragu untuk berlatih lebih banyak soal agar kemampuan Anda semakin terasah! Semoga sukses!

Related Post