Contoh Soal Persamaan Linear Dua Variabel

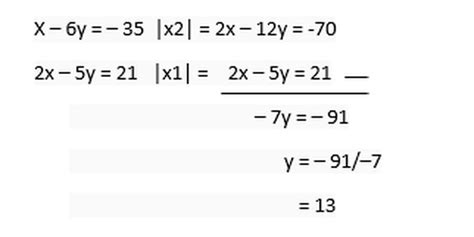
Contoh Soal Persamaan Linear Dua Variabel: Latihan dan Pembahasan

Artikel ini akan membahas contoh soal persamaan linear dua variabel beserta penyelesaiannya. Persamaan linear dua variabel merupakan salah satu materi penting dalam matematika yang sering dijumpai di sekolah menengah. Memahami konsep ini sangat krusial untuk menguasai materi matematika selanjutnya. Kita akan mempelajari berbagai tipe soal, mulai dari yang sederhana hingga yang lebih kompleks. Siap untuk mengasah kemampuanmu?

Pengertian Persamaan Linear Dua Variabel

Sebelum membahas contoh soal persamaan linear dua variabel, mari kita ingat kembali pengertiannya. Persamaan linear dua variabel adalah persamaan yang memiliki dua variabel dengan pangkat tertinggi satu. Bentuk umumnya adalah ax + by = c, di mana a, b, dan c adalah konstanta (bilangan), dan x dan y adalah variabel.

Metode Penyelesaian Persamaan Linear Dua Variabel

Ada beberapa metode yang dapat digunakan untuk menyelesaikan persamaan linear dua variabel, antara lain:

1. Metode Substitusi: Mengganti salah satu variabel dengan nilai yang dihitung dari persamaan lain.
2. Metode Eliminasi: Menghilangkan salah satu variabel dengan cara menjumlahkan atau mengurangkan kedua persamaan.
3. Metode Gabungan: Menggabungkan metode substitusi dan eliminasi.
4. Metode Grafik: Mencari titik potong dari dua garis yang mewakili persamaan.

Contoh Soal Persamaan Linear Dua Variabel dan Penyelesaiannya

Berikut beberapa contoh soal persamaan linear dua variabel dengan berbagai tingkat kesulitan:

Contoh 1 (Metode Substitusi):

Tentukan nilai x dan y yang memenuhi sistem persamaan berikut:

x + y = 5

x - y = 1

Penyelesaian:

Dari persamaan pertama, kita dapat menuliskan x = 5 - y. Substitusikan nilai x ini ke persamaan kedua:

(5 - y) - y = 1

5 - 2y = 1

2y = 4

y = 2

Substitusikan y = 2 ke persamaan x = 5 - y:

x = 5 - 2

x = 3

Jadi, solusi dari sistem persamaan tersebut adalah x = 3 dan y = 2.

Contoh 2 (Metode Eliminasi):

Tentukan nilai x dan y yang memenuhi sistem persamaan berikut:

2x + 3y = 12

x - y = 1

Penyelesaian:

Kalikan persamaan kedua dengan 2, sehingga menjadi 2x - 2y = 2. Kurangkan persamaan ini dari persamaan pertama:

(2x + 3y) - (2x - 2y) = 12 - 2

5y = 10

y = 2

Substitusikan y = 2 ke persamaan x - y = 1:

x - 2 = 1

x = 3

Jadi, solusi dari sistem persamaan tersebut adalah x = 3 dan y = 2.

Contoh 3 (Soal Cerita):

Jumlah dua buah bilangan adalah 20, sedangkan selisihnya adalah 4. Tentukan kedua bilangan tersebut.

Penyelesaian:

Misalkan kedua bilangan tersebut adalah x dan y. Maka kita dapat membentuk sistem persamaan:

x + y = 20

x - y = 4

Dengan menggunakan metode eliminasi atau substitusi, kita peroleh x = 12 dan y = 8. Jadi, kedua bilangan tersebut adalah 12 dan 8.

Latihan Soal

Coba kerjakan soal-soal berikut untuk menguji pemahamanmu:

Tanya Jawab

Q: Apa itu persamaan linear dua variabel?

A: Persamaan linear dua variabel adalah persamaan matematika yang mengandung dua variabel dengan pangkat tertinggi satu, umumnya ditulis dalam bentuk ax + by = c.

Q: Apa saja metode untuk menyelesaikan persamaan linear dua variabel?

A: Beberapa metode yang umum digunakan adalah metode substitusi, eliminasi, gabungan, dan grafik.

Q: Di mana kita bisa menemukan soal-soal latihan persamaan linear dua variabel?

A: Kamu dapat menemukan berbagai contoh soal persamaan linear dua variabel di buku teks matematika, situs web pendidikan, dan aplikasi belajar online. Artikel ini juga memberikan beberapa contoh soal persamaan linear dua variabel dan penyelesaiannya.

Semoga artikel ini bermanfaat dan membantu kamu memahami contoh soal persamaan linear dua variabel dengan lebih baik. Jangan ragu untuk berlatih lebih banyak agar semakin mahir!