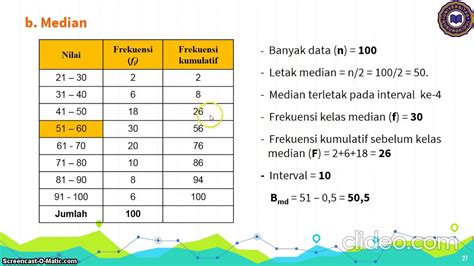
Contoh Soal Teorema Pythagoras: Pembahasan Lengkap
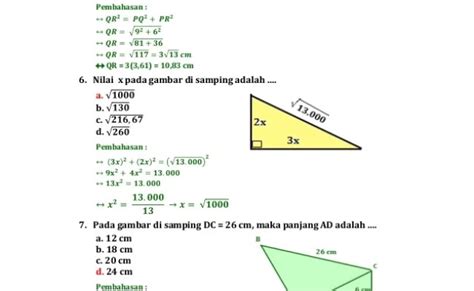
Yuk, kuasai teorema Pythagoras dengan contoh soal dan pembahasannya yang mudah dipahami! Artikel ini akan membantu kamu memahami konsep dasar dan penerapan rumus Pythagoras dalam menyelesaikan berbagai macam soal geometri. Siap-siap mengasah kemampuanmu!
Memahami Teorema Pythagoras
Teorema Pythagoras adalah teorema fundamental dalam geometri yang menjelaskan hubungan antara sisi-sisi dalam sebuah segitiga siku-siku. Teorema Pythagoras menyatakan bahwa kuadrat sisi miring (hipotenusa) sama dengan jumlah kuadrat kedua sisi lainnya (sisi tegak). Rumusnya dapat ditulis sebagai: a² + b² = c², di mana c adalah panjang hipotenusa, dan a dan b adalah panjang sisi-sisi tegak.
Contoh Soal Teorema Pythagoras #1: Segitiga Siku-Siku Sederhana
Sebuah segitiga siku-siku memiliki sisi tegak sepanjang 3 cm dan 4 cm. Berapakah panjang sisi miringnya?
Pembahasan:
- Identifikasi sisi-sisi segitiga: a = 3 cm, b = 4 cm, c = ?
- Gunakan rumus Pythagoras: a² + b² = c²
- Substitusikan nilai: 3² + 4² = c²
- Hitung: 9 + 16 = c² => 25 = c²
- Akar kuadrat kedua ruas: c = √25 = 5 cm
- Identifikasi sisi-sisi segitiga: a = ?, b = 6 cm, c = 10 cm
- Gunakan rumus Pythagoras: a² + b² = c²
- Substitusikan nilai: a² + 6² = 10²
- Hitung: a² + 36 = 100
- Kurangi 36 dari kedua ruas: a² = 64
- Akar kuadrat kedua ruas: a = √64 = 8 cm
- Identifikasi sisi-sisi segitiga: a = 3 m, b = ?, c = 5 m
- Gunakan rumus Pythagoras: a² + b² = c²
- Substitusikan nilai: 3² + b² = 5²
- Hitung: 9 + b² = 25
- Kurangi 9 dari kedua ruas: b² = 16
- Akar kuadrat kedua ruas: b = √16 = 4 m
Jadi, panjang sisi miring segitiga tersebut adalah 5 cm.
Contoh Soal Teorema Pythagoras #2: Mencari Panjang Sisi Tegak
Sebuah segitiga siku-siku memiliki sisi miring sepanjang 10 cm dan salah satu sisi tegak sepanjang 6 cm. Berapakah panjang sisi tegak lainnya?
Pembahasan:
Jadi, panjang sisi tegak lainnya adalah 8 cm.
Contoh Soal Teorema Pythagoras #3: Penerapan dalam Masalah Kehidupan Nyata
Sebuah tangga sepanjang 5 meter disandarkan pada dinding. Alas tangga berada 3 meter dari dinding. Berapa tinggi dinding yang dicapai tangga?
Pembahasan:
Ini merupakan aplikasi teorema Pythagoras dalam kehidupan nyata. Tangga, dinding, dan tanah membentuk segitiga siku-siku.
Jadi, tangga mencapai ketinggian 4 meter di dinding.
Tanya Jawab Seputar Teorema Pythagoras
Q: Apa itu hipotenusa dalam teorema Pythagoras?
A: Hipotenusa adalah sisi terpanjang dalam sebuah segitiga siku-siku, dan selalu berada di hadapan sudut siku-siku (90 derajat). Dalam rumus a² + b² = c², c mewakili panjang hipotenusa.
Q: Bisakah teorema Pythagoras digunakan pada segitiga sembarang?
A: Tidak, teorema Pythagoras hanya berlaku untuk segitiga siku-siku.
Q: Bagaimana jika saya ingin mencari panjang sisi tegak, bukan hipotenusa?
A: Anda tetap dapat menggunakan rumus a² + b² = c², hanya saja Anda perlu mengisolasi variabel yang ingin Anda cari (a atau b) sebelum menghitung.
Dengan memahami contoh soal teorema Pythagoras di atas, diharapkan Anda dapat lebih memahami dan mengaplikasikan teorema ini dalam berbagai soal geometri. Jangan ragu untuk berlatih lebih banyak soal untuk mengasah kemampuan Anda!