Contoh Soal Identitas Trigonometri: Kuasai Rumus Trigonometri!

2025-02-14 by admin
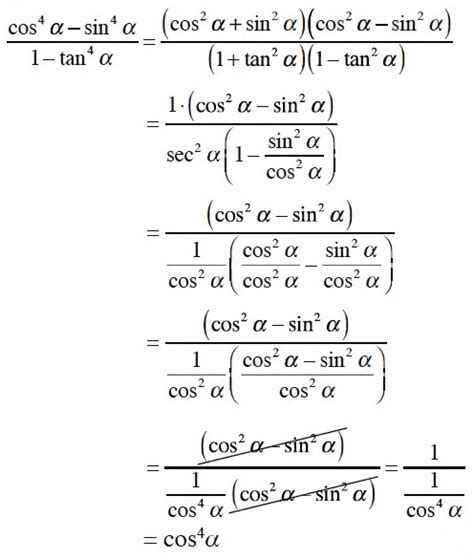
Contoh Soal Identitas Trigonometri: Kuasai Rumus Trigonometri!

Menguasai Identitas Trigonometri dengan Contoh Soal

Artikel ini menyediakan berbagai contoh soal identitas trigonometri yang disertai dengan penyelesaian langkah demi langkah. Dengan memahami identitas trigonometri, kamu akan mampu menyelesaikan soal-soal matematika yang lebih kompleks, khususnya di bidang trigonometri. Yuk, kita mulai!

Rumus-Rumus Penting Identitas Trigonometri

Sebelum masuk ke contoh soal identitas trigonometri, mari kita ulas beberapa rumus dasar yang penting:

    1. Identitas dasar:

      2. * sin²x + cos²x = 1

      * tan x = sin x / cos x

      * cot x = cos x / sin x

      * sec x = 1 / cos x

      * csc x = 1 / sin x

    2. Identitas sudut ganda:

      3. * sin 2x = 2 sin x cos x

      * cos 2x = cos²x - sin²x = 1 - 2sin²x = 2cos²x - 1

      * tan 2x = (2 tan x) / (1 - tan²x)

      Contoh Soal Identitas Trigonometri dan Pembahasannya

      Berikut beberapa contoh soal identitas trigonometri beserta penyelesaiannya:

      Soal 1: Sederhanakanlah ekspresi sin²x + cos²x + tan²x.

      Penyelesaian:

      Kita tahu bahwa sin²x + cos²x = 1. Maka ekspresi tersebut menjadi:

      1 + tan²x = 1 + sin²x/cos²x = (cos²x + sin²x) / cos²x = 1/cos²x = sec²x

      Jadi, jawabannya adalah sec²x.

      Soal 2: Buktikan identitas trigonometri: (1 + tan x)² = sec²x + 2tan x

      Penyelesaian:

      Kita mulai dari ruas kiri:

      (1 + tan x)² = 1 + 2tan x + tan²x

      Kita tahu bahwa 1 + tan²x = sec²x. Maka:

      1 + 2tan x + tan²x = sec²x + 2tan x

      Terbukti, ruas kiri sama dengan ruas kanan.

      Soal 3: Tentukan nilai dari sin 2x jika sin x = 3/5 dan x berada di kuadran I.

      Penyelesaian:

      Kita gunakan rumus sudut ganda sin 2x = 2 sin x cos x.

      Karena sin x = 3/5, kita dapat mencari cos x menggunakan identitas sin²x + cos²x = 1:

      cos²x = 1 - sin²x = 1 - (3/5)² = 16/25

      cos x = 4/5 (karena x di kuadran I)

      Maka, sin 2x = 2 (3/5) (4/5) = 24/25

      Jadi, sin 2x = 24/25.

      Tips Menguasai Identitas Trigonometri

    3. Latihan Terus Menerus: Praktik adalah kunci utama! Semakin banyak soal yang kamu kerjakan, semakin mahir kamu dalam mengaplikasikan rumus identitas trigonometri.

    4. Pahami Konsep Dasar: Pastikan kamu memahami konsep dasar trigonometri sebelum mempelajari identitas trigonometri yang lebih kompleks.

    5. Manfaatkan Sumber Belajar: Gunakan berbagai sumber belajar seperti buku teks, video tutorial, dan website edukatif untuk membantu pemahamanmu.

Tanya Jawab

Q: Apakah ada cara mudah untuk menghafal rumus identitas trigonometri?

A: Tidak ada cara instan, namun dengan sering menggunakan dan mengerjakan soal, rumus-rumus tersebut akan terpatri di ingatan. Buatlah catatan rumus dan ulas secara berkala.

Q: Bagaimana jika saya menemui soal identitas trigonometri yang rumit?

A: Cobalah untuk menyederhanakan ekspresi dengan menggunakan rumus-rumus dasar dan identitas trigonometri yang telah kamu pelajari. Jika masih kesulitan, cobalah untuk memecah soal menjadi bagian-bagian yang lebih kecil.

Semoga contoh soal identitas trigonometri di atas bermanfaat untuk membantu kamu dalam memahami dan menguasai materi ini! Jangan ragu untuk berlatih lebih banyak lagi!

Related Post