Contoh Soal Integral Tak Tentu: Panduan Lengkap

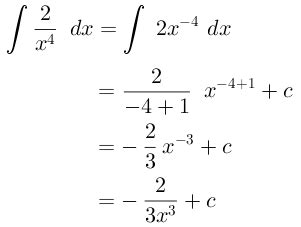
Yuk, kuasai integral tak tentu dengan latihan soal yang beragam! Artikel ini memberikan contoh soal integral tak tentu mulai dari yang paling dasar hingga yang lebih kompleks, lengkap dengan langkah-langkah penyelesaiannya. Siap mengasah kemampuan kalkulus Anda?

Contoh Soal Integral Tak Tentu: Tingkat Dasar

Integral tak tentu merupakan kebalikan dari proses diferensial. Mempelajari contoh soal integral tak tentu sangat penting untuk menguasai konsep kalkulus integral. Berikut beberapa contoh soal integral tak tentu tingkat dasar:

Soal 1: ∫ 2x dx

Penyelesaian:

Ingat rumus dasar integral ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C, dengan C adalah konstanta integrasi. Maka:

∫ 2x dx = 2 ∫ x dx = 2 (x¹⁺¹)/(1+1) + C = 2 (x²)/2 + C = x² + C

Soal 2: ∫ (3x² + 5) dx

Penyelesaian:

Kita dapat mengintegralkan setiap suku secara terpisah:

∫ (3x² + 5) dx = ∫ 3x² dx + ∫ 5 dx = 3 ∫ x² dx + 5 ∫ dx = 3 * (x³/3) + 5x + C = x³ + 5x + C

Soal 3: ∫ (4/x) dx

Penyelesaian:

Rumus integral untuk 1/x adalah ln|x| + C. Jadi:

∫ (4/x) dx = 4 ∫ (1/x) dx = 4 ln|x| + C

Contoh Soal Integral Tak Tentu: Tingkat Menengah

Berikut beberapa contoh soal integral tak tentu yang sedikit lebih menantang:

Soal 4: ∫ (x³ - 2x + 7) dx

Penyelesaian:

Integrasikan setiap suku:

∫ (x³ - 2x + 7) dx = (x⁴/4) - x² + 7x + C

Soal 5: ∫ (√x + 1/√x) dx

Penyelesaian:

Ubah bentuk akar menjadi pangkat pecahan:

∫ (x^1/2 + x^-1/2) dx = (x^3/2)/(3/2) + (x^1/2)/(1/2) + C = (2/3)x^3/2 + 2x^1/2 + C = (2/3)√x³ + 2√x + C

Contoh Soal Integral Tak Tentu: Tingkat Lanjut (Menggunakan Substitusi)

Soal 6: ∫ 2x(x² + 1)³ dx

Penyelesaian:

Gunakan metode substitusi. Misalkan u = x² + 1, maka du = 2x dx. Substitusikan ke integral:

∫ 2x(x² + 1)³ dx = ∫ u³ du = (u⁴)/4 + C. Substitusikan kembali u = x² + 1:

= (x² + 1)⁴/4 + C

Tips Menguasai Integral Tak Tentu

1. Pahami rumus dasar: Kuasai rumus integral dasar seperti yang ditunjukkan pada contoh di atas.
2. Latihan konsisten: Kerjakan sebanyak mungkin contoh soal integral tak tentu.
3. Gunakan metode substitusi: Pelajari dan praktikkan metode substitusi untuk menyelesaikan soal yang lebih kompleks.
4. Konsultasikan sumber belajar: Gunakan buku teks, video tutorial, atau sumber belajar online lainnya jika mengalami kesulitan.

Tanya Jawab

Q: Apa perbedaan integral tentu dan integral tak tentu?

A: Integral tentu menghasilkan nilai numerik, sedangkan integral tak tentu menghasilkan fungsi + konstanta integrasi (C). Integral tentu merepresentasikan luas daerah, sementara integral tak tentu merepresentasikan keluarga fungsi yang turunannya sama dengan fungsi integran.

Q: Apa pentingnya konstanta integrasi (C) dalam integral tak tentu?

A: Konstanta integrasi (C) penting karena menunjukkan bahwa terdapat banyak fungsi yang memiliki turunan yang sama. Contohnya, turunan dari x² + 2 dan x² + 5 adalah sama yaitu 2x.

Semoga artikel ini membantu Anda memahami contoh soal integral tak tentu. Jangan ragu untuk berlatih dan memperdalam pemahaman Anda! Untuk mempelajari lebih lanjut tentang topik kalkulus lainnya, silahkan baca artikel tentang diferensial. (Pastikan untuk mengganti linkkeartikeldiferensial dengan link artikel yang relevan jika ada).